Оценка продолжительности операций, включенных в сетевой график, проводится на основе затрат времени, требуемого для решения всех задач, составляющих набор работ операции. Далее выполняется прямой и обратный анализ сетевого графика, который позволит определить:
Прямой анализ начинается с первой операции проекта, проходя по всем путям сетевого графика до последней операции проекта. По мере продвижения к ранним срокам начала операций проводится добавление времени выполнения операции. EF=ES+tопер.(7.1)
Если следующая операция является операцией слияния, то ES для этой операции определяется из условия ESi=max{EFj}, j < i (7.2)
Обратный анализ начинается с последней операции. По мере продвижения по всем путям сетевого графика рассчитываются поздние сроки начала и окончания операций LS=LF – tопер. (7.3)
Если предыдущая операция является операцией ветвления, то LF для этой операции определяется из условия LFi=min{LSj}, j > i. (7.4)
Определение ранних и поздних сроков необходимо для вычисления резервов времени выполнения работ проекта SL=LS– ES=LF– EF. (7.5)
Последовательность работ, имеющих минимальный или нулевой резерв времени, составляет критический путь проекта. Критический путь показывает минимальное время необходимое для завершения проекта в целом. Пример 7.1
Таблица 7.1 – Исходные данные по проекту
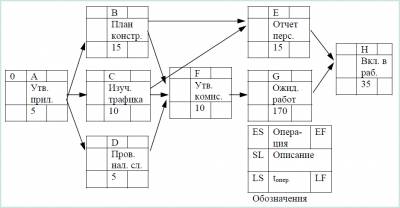
На рисунке 7.2 изображен сетевой график, построенный по исходным данным из таблицы 7.1. На рисунках 7.3 – 7.5 представлены результаты прямого анализа сетевого графика, обратного анализа и анализа резервов времени соответственно. На основании проведенного прямого и обратного анализа сетевого графика проекта установлено, что продолжительность проекта 235 единиц времени. Критический путь проекта состоит из операций А, С, F, G, H. Рисунок 7.2 – Сетевой график проекта
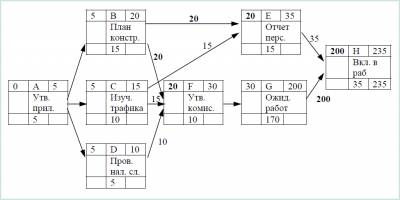
Рисунок 7.3 – Результаты прямого анализа сетевого графика
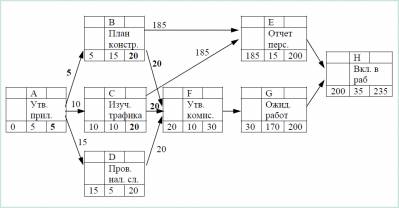
Рисунок 7.4 – Результаты обратного анализа сетевого графика
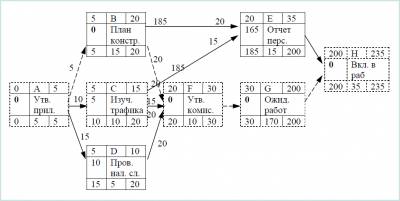
Рисунок 7.5 – Результаты расчета резервов времени
| |||||||||||||||||||||||||||||||||||||||